Quiz 2-3¶

Date: 2/26

Time: 60 min

Topics: C++, Haskell, SQL, Dijkstra's Algorithm

Allowed / prohibited resources: This quiz is open-book. You can refer to examples/solutions from previous assignments. But you cannot copy code from the internet nor discuss with classmates. (If you do either of these two things, it will probably show in your code, and you'll get a 0 -- so don't chance it.)

Submission: On this quiz, you'll need to write functions in C++ and Haskell. Write these functions in repl.it, turn in your repl.it links, and also copy/paste your actual repl.it code into the submission box as evidence that your code hasn't been modified since submitting the quiz.

Problem 1 (C++; 25% of grade)¶

Write a C++ function calcIndex(n) to find the index of the first Fibonacci number that is greater than an input number $n.$

Recall that the Fibonacci numbers are

$$a_0=0, \, a_1=1, \, a_2=1, \, a_3=2, \, a_4=3, \, a_5=5, \, a_6=8, \, a_7 = 13, \ldots$$

(every number is the sum of the previous two).

For example, if $n=8,$ then we'd have calcIndex(8)=7 because $a_7=13$ is the first Fibonacci number that is greater than $n=8.$

Make your code efficient. DON'T re-compute all the preceding values of the Fibonacci sequence each time you need to get the next values.

# include <iostream>
# include <cassert>

// write your function calcIndex here

int main()
{
    std::cout << "Testing...\n";

    assert(calcIndex(8)==7);
    assert(calcIndex(100000)==26);

    std::cout << "Success!";

    return 0;
}

Problem 2 (Haskell; 25% of grade)¶

Write a Haskell function calcGPA that takes a list of letter grades (A, B, C, D, F) and returns the GPA. The conversion is A=4, B=3, C=2, D=1, F=0.

Test your function with the following test-case:

>>> calcGPA(["A", "B", "B", "C", "C", "C", "D", "F"])
2.125

Here, the underlying computation is (4+3+3+2+2+2+1+0)/8

Problem 3 (SQL; 25% of grade)¶

On sqltest.net, given the following tables, write a query that gives (first name, last name, age, grade) for all students who got a grade of C or better. Sort the results by grade (highest grade first).

CREATE TABLE age ( 
id INT(6) UNSIGNED AUTO_INCREMENT PRIMARY KEY, 
lastname VARCHAR(30), 
age VARCHAR(30)
); 

INSERT INTO `age` (`id`, `lastname`, `age`)
VALUES ('1', 'Walton', '12'); 

INSERT INTO `age` (`id`, `lastname`, `age`)
VALUES ('2', 'Sanchez', '13'); 

INSERT INTO `age` (`id`, `lastname`, `age`)
VALUES ('3', 'Ng', '14'); 

INSERT INTO `age` (`id`, `lastname`, `age`)
VALUES ('4', 'Smith', '15'); 

INSERT INTO `age` (`id`, `lastname`, `age`)
VALUES ('5', 'Shenko', '16'); 

CREATE TABLE name ( 
id INT(6) UNSIGNED AUTO_INCREMENT PRIMARY KEY, 
firstname VARCHAR(30), 
lastname VARCHAR(30)
); 

INSERT INTO `name` (`id`, `firstname`, `lastname`)
VALUES ('1', 'Franklin', 'Walton'); 

INSERT INTO `name` (`id`, `firstname`, `lastname`)
VALUES ('2', 'Sylvia', 'Sanchez'); 

INSERT INTO `name` (`id`, `firstname`, `lastname`)
VALUES ('3', 'Harry', 'Ng'); 

INSERT INTO `name` (`id`, `firstname`, `lastname`)
VALUES ('4', 'Ishmael', 'Smith'); 

INSERT INTO `name` (`id`, `firstname`, `lastname`)
VALUES ('5', 'Kinga', 'Shenko'); 

CREATE TABLE grade ( 
id INT(6) UNSIGNED AUTO_INCREMENT PRIMARY KEY, 
firstname VARCHAR(30), 
grade VARCHAR(30)
); 

INSERT INTO `grade` (`id`, `firstname`, `grade`)
VALUES ('1', 'Franklin', 'A'); 

INSERT INTO `grade` (`id`, `firstname`, `grade`)
VALUES ('2', 'Sylvia', 'C'); 

INSERT INTO `grade` (`id`, `firstname`, `grade`)
VALUES ('3', 'Harry', 'D'); 

INSERT INTO `grade` (`id`, `firstname`, `grade`)
VALUES ('4', 'Ishmael', 'F'); 

INSERT INTO `grade` (`id`, `firstname`, `grade`)
VALUES ('5', 'Kinga', 'B');

Problem 4 (Neural Net; 25% of grade)¶

Use Dijkstra's algorithm to compute the d-values for the nodes in the following graph relative to the initial node $0.$ Work out this problem by hand.

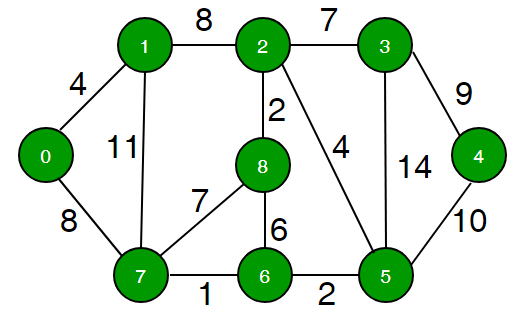
d-value of node 0: ___
d-value of node 1: ___
d-value of node 2: ___
d-value of node 3: ___
d-value of node 4: ___
d-value of node 5: ___
d-value of node 6: ___
d-value of node 7: ___
d-value of node 8: ___

Quiz 2-2¶

Date: 2/11

Time: 45 min

Topics: C++, Haskell

Allowed / prohibited resources: This quiz is open-book. You can refer to examples/solutions from previous assignments. But you cannot copy code from the internet nor discuss with classmates. (If you do either of these two things, it will probably show in your code, and you'll get a 0 -- so don't chance it.)

Submission: On this quiz, you'll need to write functions in C++ and Haskell. Write these functions in repl.it, turn in your repl.it links, and also copy/paste your actual repl.it code into the submission box as evidence that your code hasn't been modified since submitting the quiz.

Problem 1 (Haskell; 33% of grade)¶

Write a function sumFactors that finds the sum of all the factors of the input number (which you can assume is a positive integer).

In Haskell, the modulo operator is
```
a `mod` b
```

Here is a code template:

-- your function(s) here
main = print(sumFactors 10) -- should come out to 1+2+5+10 = 18

Problem 2 (C++; 66% of grade)¶

Consider the recursive sequence $$ a_{n} = a_{n-1} + 2a_{n-2}, \quad a_0=0, a_1=1. $$

The first few terms are

[a0,a1,a2,a3,a4,a5,a6,a7,a8]
[0, 1, 1, 3, 5, 11,21,43,85]

Important: A code template is provided at the bottom of the problem.

a. Write a C++ function seqSum to find the sum of the first $N$ terms without repeating any computations.

You'll need to use an array
Examples below:

seqSum(0) = a_0 = 0

seqSum(3) = a_0 + a_1 + a_2 + a_3
          =  0  +  1  +  1  +  3
          =  5

seqSum(8) = a_0 + a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7 + a_8
          =  0  +  1  +  1  +  3  +  5  + 11  + 21  + 43  + 85
          =  170

b. Write a C++ function extendedSeqSum that finds the sum of the first $N$ terms, and then finds the sum of THAT many terms without repeating any computations.

You can copy your code from seqSum and then add more onto it.
Examples below:

extendedSeqSum(2) = 1
a_2 = 1, so compute the sum through a_1

     a_0 + a_1
    = 0  +  1
    = 1

extendedSeqSum(4) = 21
a_4 = 5, so compute the sum through a_5

     a_0 + a_1 + a_2 + a_3 + a_4 + a_5
    = 0  +  1  +  1  +  3  +  5  +  11
    = 21

C++ Template

# include <iostream>
# include <cassert>

// write your functions seqSum and extendedSeqSum here

int main()
{
    std::cout << "Testing...\n";

    assert(seqSum(0)==0);
    assert(seqSum(3)==5);
    assert(seqSum(8)==170);

    assert(extendedSeqSum(2)==1);
    assert(extendedSeqSum(4)==21);

    std::cout << "Success!";

    return 0;
}

Quiz 2-1¶

Date: 1/29

Time: 45 min

Topics: Breadth-first search, depth-first search, linear regression, logistic regression, interaction terms.

List the nodes of a graph in breadth-first and depth-first orders

Fill in code tempates for breadth-first search and depth-first search
Answer conceptual questions about similarities and differences between linear and logistic regression and interaction terms

Question 1¶

Consider the following tree graph. Assume that all edges are directed downwards (so 6 is the root node).

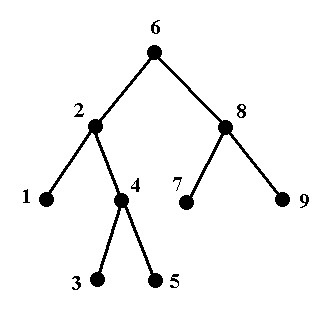
a. Give a depth-first ordering of nodes, starting with the root node.

b. Give a breadth-first ordering of nodes, starting with the root node.

c. Consider the following ordering: $6,2,4,3,5,8,7,9,1.$ Is this a breadth-first ordering, a depth-first ordering, or neither?

d. Consider the following ordering: $6, 8, 2, 7, 4, 9, 1, 3, 5.$ Is this a breadth-first ordering, a depth-first ordering, or neither?

Question 2¶

Fill in the following code for methods of a Tree class that return arrays of nodes in breadth-first and depth-first order, respectively. Note that you will not need to use any attributes of Tree. Copy and paste the template below and fill in the blanks.

def breadth_first_tranversal(self, starting_node):
... visited_nodes = []
... _____ = _____ # initialize the important data structure
... while _____:
... ... current_node = _____
... ... for child_node in current_node.children:
... ... ... __________ # update the important data structure
... ... __________ # update the important data structure again
... ... visited_nodes.append(_____)
... return _____
.
def depth_first_tranversal(self, starting_node):
... visited_nodes = []
... _____ = _____ # initialize the important data structure
... while _____:
... ... current_node = _____
... ... for child_node in current_node.children:
... ... ... __________ # update the important data 
structure
... ... __________ # update the important data structure again
... ... visited_nodes.append(_____)
... return _____

Question 3¶

a.

(i) How can you tell when you need to use logistic regression instead of linear regression?

(ii) Describe a situation different from the sandwich situation where you'd want to use logistic regression instead of linear regression.

b.

(i) What are interaction terms in the context of regression, and why are they sometimes needed?

(ii) Give a situation different from the sandwich situation where you'd want to use interaction terms.

Question 4 (Bonus)¶

Identify the 2 major shortcomings of the SIR model, construct a system for an extended SIR model that overcomes both of those shortcomings, and justify why your model overcomes those shortcomings.

Final 1¶

Date: 12/17

Time: 120 min

SUPER IMPORTANT: There are 65 short questions on this final. Most of these questions should take no more than 30 seconds to a minute if you know what you're doing. To ensure that you maximize the number of questions you're able to answer, SKIP ANY QUESTIONS THAT AREN'T IMMEDIATELY CLEAR TO YOU and come back to them only after you've gone through all the questions in the test.

Question 1 (30 points)¶

True/False. Determine whether the following statements are true or false. If false, then explain why with a single sentence. If true, then you don't have to write any additional justification.

Two events $A$ and $B$ are independent if $P(A \cap B) = 0.$
Two events $A$ and $B$ are disjoint if $P(A \cup B) = P(A) + P(B).$
If $X \sim \mathcal{U}[a,b],$ then $\textrm E[X] = \dfrac{(b-a)^2}{12}.$
In general, $\textrm{E}[X + Y] = \textrm E[X] + \textrm E[Y].$
In general, $\textrm{Var}[X + Y] = \textrm{Var}[X] + \textrm{Var}[Y].$
In general, $\textrm{Var}[X] = \textrm E[X^2] - \textrm E[X]^2.$
Standard deviation is defined as $\textrm{STD}[X] = \sqrt{\textrm{Var}[X]},$ and because you can't take the square root of a negative number, there are some distributions for which the standard deviation is undefined.
For two integers $a$ and $b,$ the expected value of the continuous uniform distribution $\mathcal{U}[a,b]$ is always equal to the expected value of the discrete uniform distribution $\mathcal{U}\{ a, a+1, \ldots, b\}.$
For two integers $a$ and $b,$ the variance of the continuous uniform distribution $\mathcal{U}[a,b]$ is always equal to the expected value of the discrete uniform distribution $\mathcal{U}\{ a, a+1, \ldots, b\}.$
"Probability mass" and "probability density" are two phrases that mean the same thing.
Because $\displaystyle \int_{-1}^3 \dfrac{1}{8} x \, \textrm{d}x = 1,$ the function $f(x) = \dfrac{1}{8} x$ represents a valid probability distribution on the interval $[-1,3].$
Given a matrix $X$ that is taller than it is wide (i.e. more rows than columns), the pseudoinverse of $X$ will always contain fewer entries than $X.$
Let $y = ax+b$ be the linear regression that is fit to a dataset $\{ (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) \}.$ Then for all $i,$ we have $y_i = ax_i + b.$
Given two probability distributions $f$ and $g,$ if the KL divergence between $f$ and $g$ is $0,$ then $f=g.$
Fitting a logistic regression is just like fitting a linear regression, except you have to transform the dependent variable first using the formula $y' = \ln \left( \dfrac{1}{y} \right) - 1.$
Given a distribution $f_k(x)$ with an unknown parameter $k,$ and some data points $\{ x_1, x_2, \ldots, x_n \}$ drawn independently from $f_k,$ the likelihood function is given by $$ P(\{ x_1, x_2, \ldots, x_n \} \, | \, k) = f_k(x_1) f_k(x_2) \cdots f_k(x_n). $$
The function $f(x,y) = \dfrac{1}{2}$ is a valid probability distribution for $(x,y) \in [0,2] \times [0,2].$
The prior distribution represents your belief before observing an event, and the posterior distribution represents your belief after observing the event.
The "posterior distribution" is always equal to the likelihood function.
Bayes' rule states that $P( A \, | \, B) = \dfrac{P(A \cap B)}{P(A)}.$
Any time it's possible to compute something recursively, you should do so, because it's always faster.
When you delete a node from a LinkedList, all you have to do is set the index of the node to None.
When you append a new node to a LinkedList, all you have to do is set its index to one more than that of the original terminal node, and set the original terminal node's next attribute to point to the new node.
If you push 3 elements onto a stack, and then pop off 2 elements, you end up with the last element you pushed.
If you push 3 elements onto a queue, and then dequeue 2 elements, you end up with the first element you pushed.
If class A inherits from class B, then any method of B is also a method of A.
The variable name i is a good name for a variable that represents a particular character in a string.
The message "Fixed everything" is a good commit message when you push to Github.
According to Python conventions, variables and functions are written in snake_case while classes are written in PascalCase.
If you can condense all of your code onto a single line, you should do that.

Question 2 (30 points)¶

Quick Answer. You DON'T have to show any work. Just state the final answer.

Suppose you have a biased coin that lands on heads two thirds of the time. If you flip the coin 3 times, what is the probability that it lands on heads exactly 2 times?
Consider the exponential distribution $p(x) = 3e^{-3x}.$ What is $\textrm E[X],$ and what is $\textrm{Var}[X]?$
Suppose $P(X \leq x) = 1-e^{-x}.$ What is $P(2 \leq x \leq 3)?$
Find the constant $c$ such that $f(x) = cx^2$ represents a valid probability distribution on the interval $[0,1].$
Find the constant $a$ such that the function $f(x) = e^x$ represents a valid probability distribution on the interval $[0, a].$
Given a matrix $X,$ what is the formula for the pseudoinverse of $X?$
What is the range of the function $\sigma(x) = \dfrac{1}{1+e^{-x}}?$
Suppose the data $\{ 2, 4, 6 \}$ are sampled from the discrete uniform distribution $\mathcal{U}\{1, 2, 3, \ldots, k\}.$ What is the likelihood $P( \{ 2, 4, 6 \} | k)$ evaluated at $k=2?$
Suppose the data $\{ 2, 4, 6 \}$ are sampled from the discrete uniform distribution $\mathcal{U}\{1, 2, 3, \ldots, k\}.$ What is the likelihood $P( \{ 2, 4, 6 \} \, | \, k)$ evaluated at $k=6?$
Suppose a coin has $P(H)=k.$ If the coin is flipped 3 times and the results are $\textrm{HHH},$ then what is the likelihood function $P(\textrm{HHH} \, | \, k)?$
Suppose a coin has $P(H)=k.$ If the coin is flipped 3 times and the results are $\textrm{HHH},$ then what is the posterior distribution $P( k \, | \, \textrm{HHH})?$
Which is faster, determinant using RREF or determinant using cofactors, and why?
Suppose that, when reducing a matrix $A$ to RREF, you divide the first row by 6, multiply the second row by 3, subtract 4 times the first row from the second row, and swap the first and second rows. If the RREF form is equal to the identity matrix, then what is $\det A?$
Consider the binary number $10101.$ What is the equivalent number in decimal form?
Consider the decimal number $25.$ What is the equivalent number in binary form?
Given that $f'(x) = 2x$ and $f(1) = 2,$ estimate $f(1.5)$ using Euler estimation with 1 step.
Using bubble sort (also known as swap sort), how many swaps are required to sort the list [4, 1, 5, 3]?
Using bubble sort (also known as swap sort), what's the maximum number of swaps required to sort a list of 4 elements?
Given the function $f(x)=x^2-1,$ carry out one iteration of the Newton-Raphson method (i.e. the "zero of tangent line" method) starting with the initial guess $x_0 = 2.$ If you were to carry out many more iterations of the Newton-Raphson method, what value of $x$ would you converge to?
Given the function $f(x)=x^2-1,$ carry out one iteration of the gradient descent starting with the initial guess $x_0 = 2$ and learning rate $\alpha = 0.1.$ If you were to carry out many more iterations of the gradient descent, what value of $x$ would you converge to?
Given the function $f(x,y)=x^2y^2 + 2(y-1)^2,$ approximate the minimum value using grid search with $x=0,1$ and $y=0, 1, 2.$
If you push elements a, b, and c onto a stack in that order, and then you run Stack.pop(), what elements remain in the stack?
If you push the elements a, b, and c onto a Queue in that order, and then you run Queue.dequeue(), what elements remain in the queue?
Suppose you're given the following edges of a tree in the form (parent, child): [(b,a), (c,d), (e,b), (f,e), (g,c), (h,f), (f,g), (h,b)]. What is the root of the tree?
How often should you push your code to GitHub?
If you run your code and see an error message that you're not familiar with, what should you do before asking for help?
If your code isn't working, but you looked at it and couldn't see any errors in logic, what should you do before asking for help?
If you ask for help in Slack, and then make a bit of progress but get stuck again, then what should you do?
What is a better variable name, conditional_probability or c_prob?
What is a better method name, LinearRegressor.coefficients() or LinearRegressor.calc_coefficients()?

Question 3 (30 points)¶

Complete the code. Copy and paste the given code template, and then fill in the blanks. Don't change the structure of the template.

Find the $n$th term of the recursive sequence $$ a_n = a_{n-1} + 2a_{n-2}, \quad a_1 = 0, \, a_2 = 3. $$

def compute_nth_term(n):
... if n == ___:
... ... return ___
... elif n == ___:
... ... return ___
... else:
... ... return ___

Replace all vowels in a string with a letter new_letter.

def replace_all_vowels(string, new_letter):
... output = ''
... for ___:
... ... if ___:
... ... ... output += ___
... ... else:
... ... ... output += ___
... return output

Multiply two matrices A and B to yield a new matrix C. You can use the attributes Matrix.num_rows and Matrix.num_columns and the methods Matrix.get_row(row_index) and Matrix.get_column(column_index) (where both of these methods return a single array that is not nested).

def dot_product(arr1, arr2):
... ans = 0
... for i in range(len(arr1)):
... ... ans += ___
... return ans
.
def matrix_multiply(A, B):
... C_elements = [[0 for _ in range(___)] for _ in range(___)]
... for col_index in ___:
... ... for row_index in ___:
... ... ... row = ___.get_row(row_index)
... ... ... column = ___.get_column(column_index)
... ... ... ___ = dot_product(row, column)
... return Matrix(C_elements)
.
Note: here, we're writing matrix_multiply as a function (not a method). To clarify, observe the following test case:
.
>>> A = Matrix([[1, 0], [0, 2]])
>>> B = Matrix([[3, 1], [0, 4]])
>>> C = matrix_multiply(A, B)
>>> C.elements
[[3, 1], [0, 8]]

Merge two sorted lists. (Assume the lists are sorted from smallest to largest.)

def merge(list1, list2):
... output = []
... i = 0 # index in list1
... j = 0 # index in list2
... while ___:
... ... if list1[i] < list2[j]:
... ... ... output.append(___)
... ... ... ___ += 1
... ... else:
... ... ... output.append(___)
... ... ... ___ += 1
... if i < ___:
... ... output += list1[i:]
... if j < ___:
... ... output += list2[j:]
... return output

Implement merge sort. You can use the merge function above as a helper function.

def merge_sort(input_list):
... if len(input_list) < ___:
... ... return input_list
... halfway_index = ___
... left_half = ___
... right_half = ___
... sorted_left_half = ___
... sorted_right_half = ___
... return ___

Quiz 1-6¶

Date: 11/19

Time: 60 min

Topics: Determinant via Cofactors vs RREF; Uniform, Exponential, & Poisson Distributions; Bayesian Inference, Linear Regression, Probability

Question 1¶

True/False. Determine whether the following statements are true or false. If false, then justify your answer. If true, then you don't have to write any additional justification.

Computing the determinant using the cofactor method is recursive, which makes it faster than computing the determinant using the RREF method.
In the exponential distribution and the Poisson distribution, the value x=0 has the smallest probability, and the probability density increases as x becomes large.
In Bayesian inference, the prior distribution represents your belief before you have observed some event, while the posterior distribution represents your belief after you have observed the event.
A linear regression is only correct if it passes through every point in the dataset.
The pseudoinverse of a matrix X is represented by $(X^T X)^{-1} X^T.$ The pseudoinverse is only defined for square matrices.

Question 2¶

Quick Answer. Answer the following questions. Justify your answer with a single sentence.

For an $n \times n$ matrix, how many computations are required to compute the determinant using the cofactor method?
Fill in the blank: The continuous uniform distribution on the interval $[1,2]$ has probability density $p(x)=\_\_$ if $1 \leq x \leq 2$ (and $0$ otherwise).
Fill in the blank: The discrete uniform distribution on the set $\{1, 2, 3\}$ has probability $p(x)=\_\_$ if $x\in \{ 1, 2, 3 \}$ (and $0$ otherwise).
Is the exponential distribution discrete or continuous? Is the Poisson distribution discrete or continuous?
Consider the discrete uniform distribution, the continuous uniform distribution, the exponential distribution, and the Poisson distribution. For which of these distributions is the variance equal to the square of the expected value?
If you are fitting a linear regression $y=a + bx$ to a dataset consisting of N points $(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N),$ you need to solve a matrix equation $X v = y$ where $v$ is the column vector $v = \begin{bmatrix} a \\ b \end{bmatrix}.$ What are the dimensions of $X?$ (How many rows, and how many columns?)

Question 3¶

Quick Computations. Answer the following questions. Show some intermediate step of work (it doesn’t have to be much, but it should be enough for me to tell what approach you’ve taken to solve the problem).

Let $p(n) = c\left( \dfrac{1}{2} \right)^n$ where $n=0, 1, 2, \ldots .$ If $N \sim p(n),$ then what is the value of $c?$
Continued from above: what is the probability that $N$ is greater than $3?$ Give an exact answer (as a fraction).
Suppose $P(X \leq x) = 1-e^{-x} if x \geq 0$ and $0$ otherwise. What is $P(3 < x < 5)?$ Give an exact answer.
On his clarinet, Squidward can play 5 songs well and 10 songs poorly. If he randomly plays 5 songs in a row, what is the probability that he plays all of the songs well? (Assume he plays a different song each time.) Round your answer to 5 decimal places.
Continued from above: what is the probability that Squidward plays exactly 2 of the songs well? Round your answer to 5 decimal places.
If $P(A) = 0.7$ and $P(B) = 0.8$ and $P(A \cup B) = 0.9,$ then what is $P(A \cap B)?$

Bonus Questions¶

Only do these if you've finished the problems above.

Continued from Quick Computation #1: What is the probability that $N$ is a multiple of 5 (including 0)? Give an exact answer (as a fraction).
Two thirds of the time, I’m here. Half of the time, I’m there. But I’m always here or there. What fraction of the time am I both here AND there?

Quiz 1-5¶

Date: 10/30

Time: 60 min

Topics: Probability Distributions, Expectation/Variance, MergeSort, Gradient Descent, Determinant

Question 1¶

Determine whether the following statements are true or false. If false, then justify your answer. If true, then you don't have to write any additional justification.

The function $f(x) = 2x$ represents a valid probability distribution on the interval $[0,1].$
The function $f(x) = x^2$ represents a valid probability distribution on the interval $[0,1].$
The expected value of a random variable $X$ is $\displaystyle\int_{-\infty}^\infty x \, p(x) \, \textrm dx$
The variance of a random variable is $X$ is $\displaystyle\int_{-\infty}^\infty (x - \textrm E[X])^2 \, p( (x - \textrm E[X])^2 ) \, \textrm dx.$
The variance of a random variable can be positive.
The variance of a random variable can be zero.
The variance of a random variable can be negative.
If $X \sim \mathcal U[a,b],$ then $\textrm E[X] = \dfrac{a+b}{2}.$
If $X \sim \mathcal U[a,b],$ then $\textrm{Var}[X] = \dfrac{(a+b)^2}{4}.$
If $X \sim p,$ where $p(x) = a e^{-ax},$ then $\textrm E[X] = a.$
If $X \sim p,$ where $p(x) = a e^{-ax},$ then $\textrm{Var}[X] = \dfrac{1}{a^2}.$
Gradient descent and Newton’s method are two techniques for estimating the zero of a function.
Given the function $f(x) = 1-x^2$ and the initial guess $x=1,$ gradient descent and Newton's method (the "zero of tangent line method") will converge to the same result.
The determinant can be obtained from the RREF process by first multiplying together the numbers you divide by, and then switching the sign of that product if there was an odd number of swaps.

Question 2¶

Given the function $f(x) = x^2-1$ and the initial guess $x=2,$ carry out $2$ iterations of gradient descent using the learning rate $\alpha = 0.1.$

If you kept going forever, what number would you converge to?

Question 3¶

Fill in the blanks in merge_sort, shown below. You may reference a function merge(a,b) which merges two sorted lists a and b into a single sorted list.

def merge_sort(arr):
... if len(arr) < ___:
... ... return ___
... halfway_index = ___
... left_half = ___
... right_half = ___
... sorted_left_half = ___
... sorted_right_half = ___
... return ___

Quiz 1-4¶

Date: 10/16

Time: 60 min

Topics: RREF, LinkedList, Newton-Raphson Method, Inverse via Augmented Matrix

Question 1¶

Determine whether the following statements are true or false. If false, then justify your answer. If true, then you don't have to write any additional justification.

In the RREF algorithm, you have to clear below for every single column except for the last column.
If a matrix is invertible, its reduced row echelon form will be the identity matrix.
To compute the inverse of an $N \times N$ matrix $A,$ you can stack the matrix $A$ on top of the identity matrix (thereby creating a $2N \times N$ augmented matrix), row reduce the augmented matrix, and take the bottom $N$ rows of the augmented matrix.
In a linked list, the nodes are stored within an array.
In a linked list, no node can have more than one next node.
When you implement a linked list, the LinkedList class inherits from the Node class.
If you use the Newton-Raphson method (i.e. the "zero of tangent line method") to find a zero a function $f(x),$ you will always converge to a zero of the function, regardless of your initial guess. (If you say false, then provide a counterexample of a function and an initial guess for which the Newton-Raphson method would not converge to a zero of the function.)
As long as you can get the output of a function for any input, you can use the Newton-Raphson method on the function, even if you don’t know the actual formula for the function.

Question 2¶

Approximate the zero of $f(x) = x^2 - 2$ using 4 iterations of the Newton-Raphson method (i.e. repeatedly using the zero of the tangent line as your next guess). Show your intermediate work at each step; please DO use a calculator for your arithmetic.

Question 3¶

Fill in the blanks in the push method below, which is part of the class LinkedList. The push method insert a new node at the head of the LinkedList, containing the new_data, and updates the head and indices of the nodes appropriately.

def push(self, new_data):
..... new_node = Node(new_data)
..... new_node.next = _____
..... self.head = _____
..... 
..... current_node = self.head
..... current_index = _____
..... while _____:
..... ..... current_node.index = _____
..... ..... current_node = _____
..... ..... current_index += 1

Quiz 1-3¶

Date: 10/2

Time: 60 min

Topics: Monte Carlo, Matrix Multiplication Algorithm, Tally Sort, KL Divergence, Inheritance

Question 1¶

Determine whether the following statements are true or false. If false, then justify your answer. If true, then you don't have to write any additional justification.

If the class Student inherits from the class Person, then the class Student receives all the attributes of Person but not all the methods of Person.
Consider an experiment in which we flip a coin $N$ times. If we create an array to represent the probability distribution of the number of heads, then the array will have $N+1$ elements.
Suppose we perform a Monte Carlo simulation to approximate the probability distribution of some experiment. As we increase the number of samples in the Monte Carlo simulation, we expect the KL divergence to increase proportionally.
In the tally sort algorithm, you don't really have to subtract off the minimum at the beginning. The algorithm will be slightly less efficient, but it will still work.
Probability is usually between 0 and 1, but it can sometimes be greater than 1.
Suppose you flip a coin $N$ times. If you plot the number of heads on the $x$-axis, and on the $y$-axis you plot the total number of flips on which $x$ heads occurred, then it will take the same overall shape as the probability distribution of the number of heads.

Question 2¶

Fill in the blanks in the matrix multiplication function below. Assume that you can refer to the number of rows or columns in a matrix A using A.num_rows or A.num_cols.

def matrix_multiply(A, B):
..... product_elements = [[0 for _ in range(___)] for _ in range(___)]
..... for col_index in range(___):
..... ..... for row_index in range(___):
..... ..... ..... dot_product = 0
..... ..... ..... for i in range(___):
..... ..... ..... ..... dot_product += ___
..... ..... ..... product_elements[row_index][col_index] = ___
..... return Matrix(product_elements)

Question 3¶

Suppose we perform a Monte Carlo simulation for the number of heads in 3 coin flips. Tell whether each of the following could be the resulting approximation for the probability distribution of the number of heads. For any instances of "no", explain why not.

$[0.25, 0.25, 0.25, 0.25]$
$[0.2, 0.2, 0.2, 0.2]$
$[0, 0.5, 0.5, 0]$
$[1, 0, 0, 0]$
$[0, 1, 1, 0]$

Quiz 1-2¶

Date: 9/18

Time: 60 min

Question 1¶

Suppose you have a fair coin (meaning it lands on heads vs tails equally).

a. If you flip the coin 6 times, what is the probability of getting 4 heads? In terms of showing your work, you just need to write down your unsimplified expression at the beginning, and then for your final answer just plug it into an online calculator and write down the corresponding decimal.

b. Let $P(N)$ represent the probability of getting $N$ heads in 6 flips. Explain your answer using logic, without actually computing all the terms in the sum.

Question 2¶

Suppose you do a Monte Carlo simulation with the following 10 samples.

H H T H T T
H H H T T H
T T H H T H
T H T T H T
H H T T H H
T H T H T T
T T H H T T
H H T T H H
T T T T H T
H T T H H T

a. According to the Monte Carlo simulation, what is the approximate probability of getting 4 heads? In terms of showing your work, just write down a single sentence to briefly explain what you did to get the result.

b. What could you change to make the Monte Carlo simulation give more accurate approximations?

c. Let $P(N)$ represent the approximated probability of getting $N$ heads in 6 flips. What is the value of $P(0) + P(1) + P(2) + P(3) + P(4) + P(5) + P(6)?$ Explain your answer using logic, without actually computing all the terms in the sum.

Question 3¶

Fill in the blanks in the following recursive implementation of swap_sort. You can copy and paste the code into the response, area and then replace the blanks with the appropriate contents.

def swap_sort(num_list):
..... ___ = 0
..... for i in range(___):
..... ..... ___ = num_list[i]
..... ..... ___ = num_list[i+1]
..... ..... if ___ > ___:
..... ..... ..... num_list[i] = ___
..... ..... ..... num_list[i+1] = ___
..... ..... ..... ___ += 1
..... if ___:
..... ..... return swap_sort(num_list)
..... else:
..... ..... return ___

Question 4¶

Do any 4 of the following. (It's possible to get some extra credit if you do all 5.)

a. Write a list comprehension that returns all of the numbers from 1 to 1000 that are divisible by 7

b. Write a list comprehension that returns all of the numbers from 1 to 1000 that have a 3 in them

c. Write a list comprehension that finds all of the words in a string that are less than 4 letters. You can use the variable string to represent the string.

d. Write a list comprehension that gives an $N \times N$ matrix such that the main diagonal and the diagonal below it consist of 1's. For example, a $4 \times 4$ matrix of this kind would be

[[1, 0, 0, 0],
 [1, 1, 0, 0],
 [0, 1, 1, 0],
 [0, 0, 1, 1]]

e. Write a list comprehension that gives a "reverse-counting" matrix with $N$ rows and $M$ columns. For example, the $2 \times 4$ "reverse-counting" matrix would be

[[8, 7, 6, 5],
 [4, 3, 2, 1]]

Quiz 1-1¶

Date: 9/4

Time: 60 min

Topics: Recursion, String Processing; Classes, Attributes, and Methods

Question 1¶

In the space below, write a recursive function nth_term that finds the nth term of a sequence $$ a_n = a_{n-1} - 2a_{n-2}, \quad a_1 = 0, \, a_2 = 3. $$

Question 2¶

a. In the space below, write a function separate_into_words that passes the following test:

>>> separate_into_words("look the dog ran fast")
["look", "the", "dog", "ran", "fast"]

b. In the space below, write a function reverse_word_order that passes the following test. You can use separate_into_words as a helper function within reverse_word_order.

>>> reverse_word_order("look the dog ran fast")
"fast ran dog the look"

Question 3¶

In the space below, write a class Student that passes the following tests:

>>> s = Student("Shelby", 6)
>>> s.name
"Shelby"
>>> s.grade
6
>>> s.greeting()
"I'm Shelby and I'm in grade 6"

>>> s = Student("Maurice", 8)
>>> s.name
"Maurice"
>>> s.grade
8
>>> s.greeting()
"I'm Maurice and I'm in grade 8"