Depth-First and Breadth-First Search

To understand what depth-first and breadth-first search are, we must first know what graphs and directed graphs are. A graph is a set of objects (often called nodes) that are connected to each other. A pair of nodes is called an edge, and edges make up the “structure” of a graph. Put simply, a graph is a set of nodes and edges. A directed graph is a special instance of a graph. The difference is that in a regular (undirected) graph, the edges are bidirectional, meaning that they don’t have a specific direction. However, in a directed graph, each edge has a specified direction.

Graphs and directed graphs can be used to model many real-life phenomena. For example, a graph can model a social network since communication between social accounts goes both ways. On the other hand, a directed graph can model cities connected by railroad tracks since each railroad track has a specific direction.

Examples of Graphs

The following picture is an example of an undirected graph:

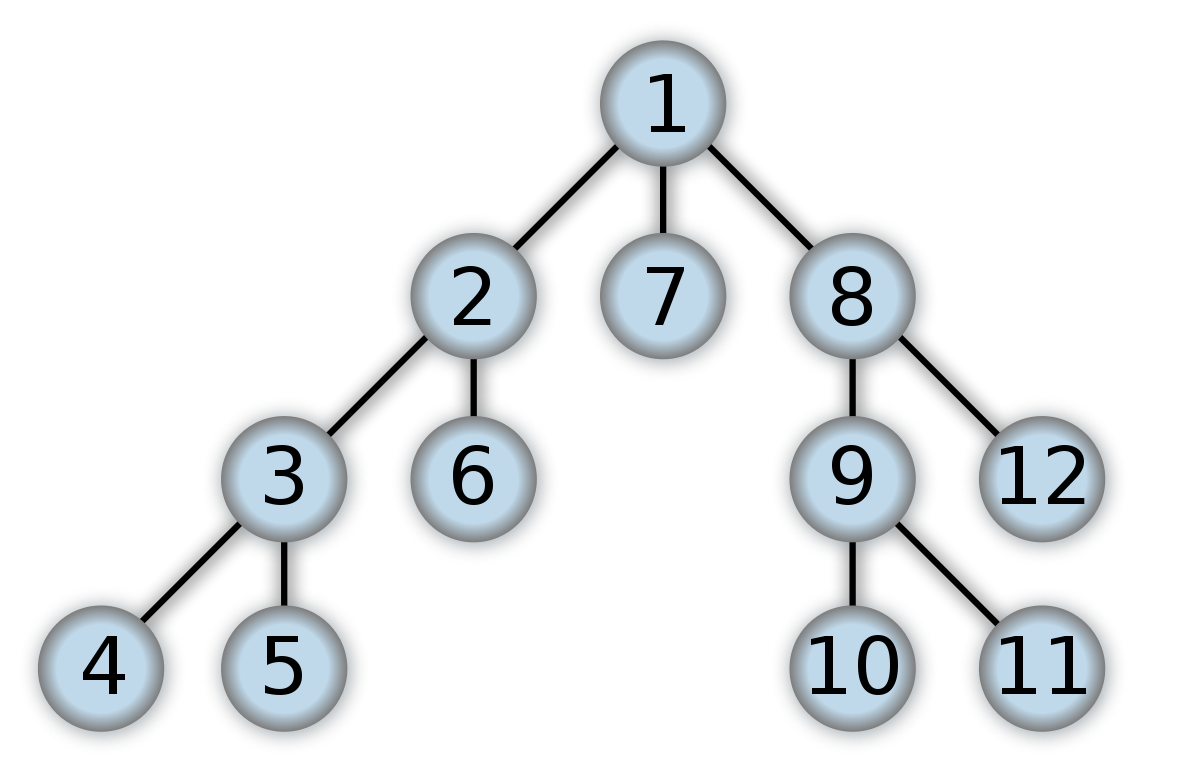
Here, the labeled circles represent nodes and the lines between the nodes represent undirected edges.

In the context of a social network, think of node 1 as yourself. The nodes 2, 7, and 8 would be your friends. The nodes 3 and 6 would be the friends of 2 and the nodes 9 and 12 would be the friends of 8. Since no other nodes are connected to 7, you are node 7’s only friend. By the same logic, nodes 4 and 5 are friends of 3 while nodes 9 and 12 are friends of 8.

The following picture is an example of a directed graph:

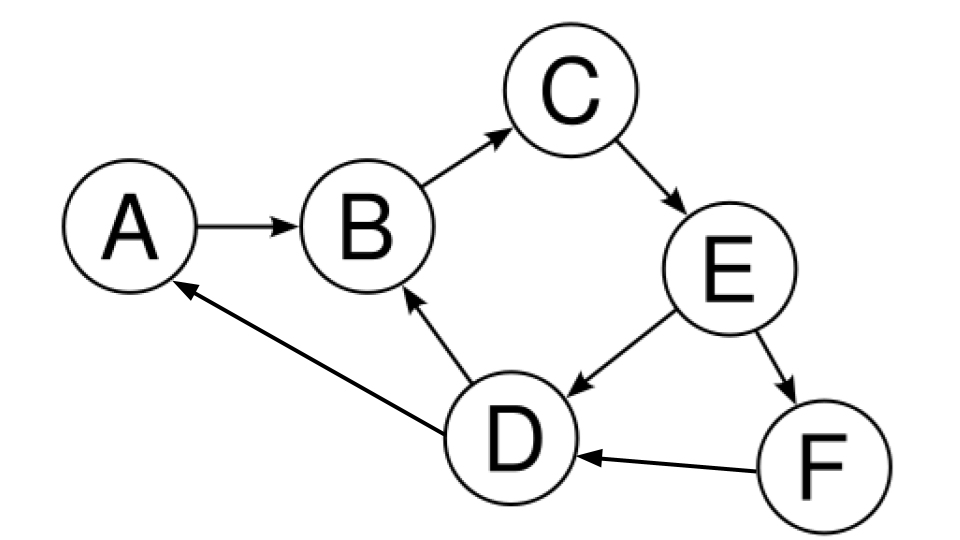
Again, the nodes are labeled circles and the edges are the lines between the nodes. However, notice that these edges have an arrow designating the direction.

In the context of cities connected by railroad tracks, node A would be your home city. The directed edge $A \to B$ represents a railroad that goes from city A to city B (but does not go back to city A). From city A, we can only go to city B. From city B, we can only go to city C (since the edge connecting B and D is $D \to B$, not $B \to D$). City C can only go to city E. When we get to city E, we can either go to city D (which in turn will allow us to loop back to city A city B) or city F (from which we can go to city D).

Depth-First and Breadth-First Search

Now that we know what graphs and directed graphs are, we can introduce depth-first and breadth-first search. As implied by the name, these methods traverse the graph by prioritizing either depth or breadth.

Depth-first search prioritizes depth. Starting at some node in the graph, we travel along one of the edges that connects to this node. This edge takes us to a new node, and we repeat the process, traveling along one of the edges that connects to the new node. This takes us deeper and deeper into the graph. Once we reach a node for which there are no more edges that we can travel along, we backtrack and go back up the graph until there is a path that we haven’t taken already. We then go deep down the path as far as possible, and then repeat the process until we’ve visited each and every node in the graph.

Breadth-first search prioritizes breadth. Instead of repeatedly traveling deep into the graph, breadth-first search has us traveling through each “layer” of the graph. If we think about a family tree diagram as an example, a “layer” would be a single generation of people. In the case of a graph, a “layer” would be a single generation of nodes, so to speak. In this context, breadth-first searching can be interpreted as traversing by “generation”, whereas depth-first searching can be interpreted as traversing by direct “branches” of the family tree.

Implementing a Graph Class

A graph class is a collection of nodes along with methods for operating on the nodes. Each node has an index and a list of “neighbors” (or “parents”, in the case of a directed graph).

To initialize a graph, we can pass in a list of edges, where each edge is a tuple of node indices. From the edges list, we can determine all the possible indices of nodes, and then create a node that corresponds to each of those indices.

class Graph:
    def __init__(self, edges):
        self.edges = edges
        indices = []

        for edge in edges:
            indices.append(edge[0])
            indices.append(edge[1])

        self.nodes = [Node(n) for n in range(max(indices) + 1)]

Now that we have initialized our graph, we are now able to build it. Building a graph involves setting the neighbors of each node.

def build_from_edges(self):
    for edge in self.edges:
    	i = edge[0]
    	j = edge[1]
        self.nodes[i].neighbors.append(self.nodes[j])
        self.nodes[j].neighbors.append(self.nodes[i])

Implementing Depth-First and Breadth-First Search

To implement a breadth-first search, we use a queue, a data structure that has elements inserted and removed according to the first-in first-out principle. Every time we visit a node, we want to add it to our queue if we haven’t visited it already. Our queue keeps track of which nodes we still need to “deal with”, so to speak. When we “deal with” a node, we add the node to our output array, add the node’s unvisited neighbors to the queue, and then finally remove the node from the queue. We continue doing this until there are no more nodes left in the queue.

def fetch_nodes_breadth_first(self, root_index):
    root_node = self.nodes[root_index]
    queue = []
    queue.append(root_node)

    visited = {}
    visited[root_node.index] = True

    result = []
    result.append(root_node)

    while len(queue) > 0:
    	node = queue[0]

        for neighbor in node.neighbors:
            if neighbor.index not in visited:
                queue.append(neighbor)
                result.append(neighbor)
                visited[neighbor.index] = True

        queue = queue[1:]

    return result

Depth-first search is similar to breadth-first search. The only difference is that instead of a queue, we use a stack, a data structure that has elements inserted and removed according to the first-in last-out principle.

def fetch_nodes_depth_first(self, root_index):
    root_node = self.nodes[root_index]
    stack = []
    stack.append(root_node)

    visited = {}
    visited[root_node.index] = True

    result = []
    result.append(root_node)

    while len(queue) > 0:
    	node = stack[-1]

        for neighbor in node.neighbors:
            if neighbor.index not in visited:
                stack.append(neighbor)
                result.append(neighbor)
                visited[neighbor.index] = True

        stack = stack[:-1]

    return result

Keep in mind that there can be different outputs for each of the search methods. In the case of breadth first search, you can switch up the order of elements on the same layer. In the case of depth first search, you can choose different paths to start going down.